Tackling Conversion With Survival Models And Neural Networks
At Better, we have spent a lot of effort modeling conversion rates using Kaplan-Meier and gamma distributions. We recently released convoys, a Python package to fit these models.Background
At Better Mortgage we rely on modeling conversion rates. We use these predictions to estimate customer acquisition costs, score leads, and even help manage our mortgage pipeline hedging strategy. Getting a mortgage isn’t instantaneous; the process starts with a visit to better.com and takes the majority of our customers at least 32 days to complete.
Since our conversion data is inherently lagged, our conversion models are variations of a survival model known as a parametric cure model (lifelines has a nice intro to cure models). We’ve also developed Convoys, which is our own Python package for doing this type of modeling. This model is generally described as:
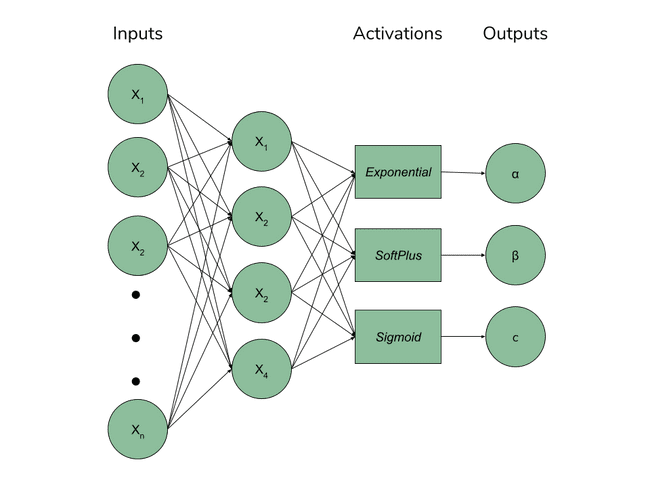
If we consider a feature vector x:
is the probability of converting at any point in the future
is a probability density function of the time to the conversion event, conditional on the conversion occurring
is the cdf of that density function
Common choices for are the Gamma, Weibull, and Exponential distributions, but any probability distribution defined over could work.
A lot of this is covered in a previous blog post, so we encourage anyone interested to check that out for further background. In summary, the benefit here is being able to:
- Use censored data when fitting a model, so we’re always incorporating the most recent user behavior in our data. We also don’t have to define an arbitrary “converted by X days” binary indicator.
- Get parameters for distributions instead of point estimates, which let us quantify our uncertainty as well as extrapolate future conversion likelihood more easily (since we have a model).
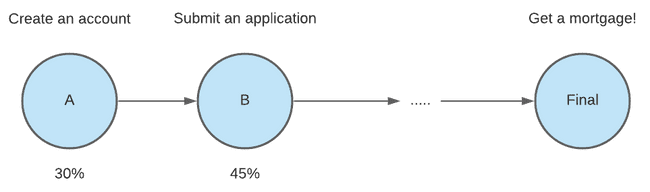
The problem with using a regression-type model such as Convoys is that they require us to use features fixed at a point in time. This becomes problematic when you have a long conversion funnel like we do. Our conversion funnel is broken down into multiple steps which we call “milestones”.
When someone applies for a mortgage, the data we have about that person is limited to information from their application. The fields on the application include things like self reported financial details and loan type preference. We can use these features to predict the likelihood that this person will choose to fund a mortgage with Better Mortgage.
However, there are a lot of things that can happen between the creation of an application and eventual funding. For example, someone who uploads all the necessary forms and documentation instantly is more likely to get a mortgage with Better Mortgage than someone who takes a few weeks, or never completes any next steps at all. Our regression style models are not able to handle these kinds of time-varying features.
Because of this, we wanted to find a way to extend our existing framework to incorporate time dependent features that still allow us to work with censored data and output distribution parameters.
Discrete Time Survival Analysis
We found that we could incorporate these time dependent features into our existing framework by reformatting our training dataset; changing the instance of prediction from a borrower to a borrower + period. These lecture notes have more detailed technical info, but the short/intuitive version is that you go from a “Person-Level” data set:
| Person | Time to convert OR time till now | Did they convert? |
|---|---|---|
| A | 3 days | 0 |
| B | 2 days | 1 |
To a “Person-Period” data set:
| Person | Period | Did they convert ever? | Time to convert OR time till now |
|---|---|---|---|
| A | Day 1 | 0 | 3 Days |
| A | Day 2 | 0 | 2 Days |
| A | Day 3 | 0 | 1 Days |
| B | Day 1 | 1 | 2 Days |
| B | Day 2 | 1 | 1 Days |
Where each “period” is an equal unit of time, representing the fact that we observed this person up to and including that period.
In theory, we can apply our existing Convoys model to this dataset with no modifications. In practice, incorporating time dependent features in a linear model like this presents you with lots of seemingly arbitrary feature engineering decisions.
For example, suppose you hypothesize that a borrower's web activity over time will have a lot of predictive value in your model. You now need to think about how you want to calculate that feature for each person-period of your dataset. Is your feature a cumulative count of page views? A cumulative count of page views but with a five day lookback? Just the page views in that period? Testing even a handful of these different features for your “borrower web activity” hypothesis takes time that would be better spent incorporating other kinds of data (like a borrower’s responses to communications).
We also found ourselves adding a lot of categorical/binary features (What’s the most recent thing the borrower did? Did they do X yet?). These features tended to have very non-linear relationships, which our linear model was not the best at capturing.
This led us to begin exploring possible alternatives for our modeling backend that could reduce some of the feature engineering overhead and better handle non-linear relationships.
Since we already have a really good objective function defined for our problem, we are able to use a neural network as the backend for fitting our existing parametric model to get the best of both worlds: a model with super flexible/non-linear relationship between features and targets as well as parameters to probability distributions we can use to characterize conversion probability. We’ll talk more about how we implemented this in our next post.
Finally...
We are hiring! If you're interested in these types of problems, definitely let us know! We have a small but quickly growing team in of data engineers/scientists in New York City who are working on many of these types of problems on a daily basis.

Our thinking
CloudFront error pages for custom origins
Tue Jan 09 2018—by Liam Buchanan3 min readI gave the business what they asked for and they never used it
An addition to the long list of unused ML projectsMon Jun 29 2020—by Kenny Ning3 min read- data
- ML
- project management
Modeling conversion rates and saving millions of dollars using Kaplan-Meier and gamma distributions
At Better, we have spent a lot of effort modeling conversion rates using Kaplan-Meier and gamma distributions. We recently released convoys, a Python package to fit these models.Mon Jul 29 2019—by Erik Bernhardsson8 min read